🔥The 9th Round of Easy Loan, Earn $40 Reward is in progress❗️ ⏰ Promotion Period: January 15th - Feburary 15th, 2025 👉 Register now and check more details at gate.io/campaigns/358

0 (Reproducing Chinchilla-optimal in a colab in an hour with theoretical guarantee) Left: From Chinchilla paper; right ours; for details, see the thread below.

1/5. Excited to share a spicy paper, "Rethinking conventional wisdom in machine learning: from generalization to scaling", arxiv.org/pdf/2409.15156. You might love it or dislike it! NotebookLM: notebooklm.google.com/notebook/43f11… While double-descent (generalization-centric,

We're excited to announce the ICML 2025 call for workshops! The CFP and submission advice can be found at: icml.cc/Conferences/20…. The deadline is Feb 10. Courtney Paquette, Natalie Schluter and I look forward to your submissions!

1. We often observe power laws between loss and compute: loss = a * flops ^ b + c 2. Models are rapidly becoming more efficient, i.e. use less compute to reach the same loss But: which innovations actually change the exponent in the power law (b) vs change only the constant (a)?

There were so many great replies to this thread, let's do a Part 2! For scaling laws between loss and compute, where loss = a * flops ^ b + c, which factors change primarily the constant (a) and which factors can actually change the exponent (b)? x.com/_katieeverett/…

This time let's look at: * More about how data affects the exponent * MoE vs Transformers * More about optimizers: NTK vs feature learning and AdamW vs Muon * Inference-time scaling

On data: Sharma & Kaplan 2020 proposes a theoretical model where data distribution and task induce the data manifold dimensionality, which in turn induces the scaling exponent. Can explain why different modality = different exponent. h/t chopwatercarry x.com/chopwatercarry…

chopwatercarry Henighan et al 2020 shows empirically that different modalities (language, image, video, math) have different exponents. Same for different image resolutions (8x8 vs 16x16 etc). (They also find that the exponent for optimal model size vs compute is universal across modalities.)

chopwatercarry Bansal et al 2022 compares the data scaling exponents on translation tasks and find the same exponent across different architectures, data filtering techniques, and synthetic i.i.d. noise. Adding non-i.i.d. noise via data augmentation (back-translation) does change the exponent.

It's very difficult to improve the *exponent* in scaling laws for loss vs compute, especially by changing the optimizer! Our new paper shows that scaling momentum correctly can *provably* improve the scaling exponent on a theoretical model. Empirically, it works on LSTMs too!

Title: Dimension-adapted Momentum Outscales SGD Link: arxiv.org/pdf/2505.16098 Work done with amazing collaborators Katie Everett Gauthier Gidel Elliot Paquette Courtney Paquette Related 🧵: x.com/_katieeverett/… x.com/_katieeverett/…

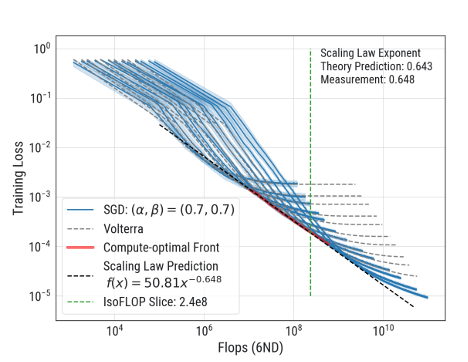
While scaling laws typically predict the final loss, we show in our ICML oral paper that good scaling rules enable accurate predictions of entire loss curves of larger models from smaller ones! w/Lechao Xiao, Andrew Gordon Wilson, J. Pennington, A. Agarwala: arxiv.org/abs/2507.02119 1/10